Section 1: Density-dependence
Growth Rate
Watch the following animation and then answer the following question using the radio buttons.
How would you describe the rate of growth of the fish population?
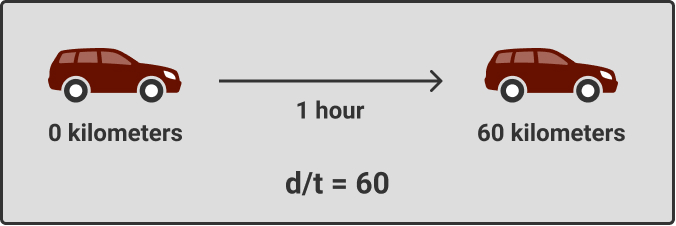
Distance of 60 kilometres (d) travelled by a car in 1 hour (t), which corresponds to a velocity or speed (d/t) of 60 km per hour.
In turn, if a population grew 10 individuals in 1 year, it would have a change over time, or growth rate, of 10 individuals per year.
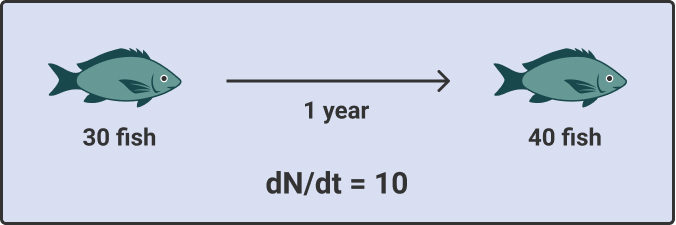
Change in a fish population size (N) from 30 fish to 40 fish in one year (t), which corresponds to a population growth rate (ΔN/Δt) of 10 fish per year.
In the figure, the growth rate (dN/dt) is the slope at any time point of the function (i.e., of the graph line).
Graphical representation of the logistic growth in the fish population that demonstrates the change in the fish population size (N) from 30 to 40 fish (ΔN = 10) within one year (Δt = 1).
Does the logistic equation look familiar? It should because it is a modified version of the exponential equation. It describes the population growth in a resource-limited environment. The equation generates the characteristic sigmoid S-shaped growth curve (as seen in the fish example). Click “Next” to go to Section 2. Carrying capacity.
Graphical representation of the logistic growth in the fish population, demonstrating the carrying capacity (K).