Section 1 : Dépendance à la densité
Taux de croissance
Regardez l’animation suivante, puis répondez à la question suivante en utilisant les boutons radio.
Comment décririez-vous le taux de croissance de la population des poissons ?
En revanche, si une population augmentait de 10 individus en un an, elle connaîtrait une évolution dans le temps, ou taux de croissance, de 10 individus par année.
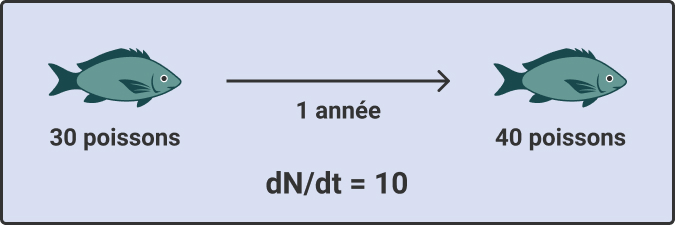
Dans la figure, le taux de croissance (dN/dt) est la pente à tout moment de la fonction (c’est-à-dire de la ligne du graphique).
Représentation graphique de la croissance logistique de la population de poissons qui démontre le changement de la taille de la population de poissons (N) de 30 à 40 poissons (ΔN = 10) en un an (ΔN = 1).
L’équation logistique vous semble-t-elle familière ? Elle devrait car il s’agit d’une version modifiée de l’équation exponentielle. Elle décrit la croissance de la population dans un environnement à ressources limitées.
L’équation génère la courbe de croissance sigmoïde caractéristique en forme de S (comme dans l’exemple des poissons).
Cliquez sur “Suivant” pour passer à la Section 2. Capacité de charge.
Représentation graphique de la croissance logistique de la population de poissons, démontrant la capacité de charge (K) avec la ligne pointillée horizontale.